
Significant stressors in one region may be trivial for the biological community of the other. behave differently than temperate streams of the mid-Atlantic. For example, arid and seasonal streams of the western U.S. Stress related to flow alteration is closely tied to temporal variability and regional flow characteristics.
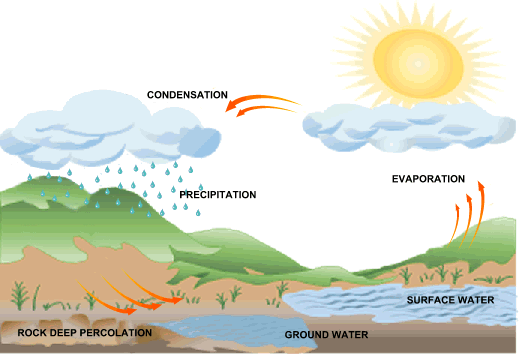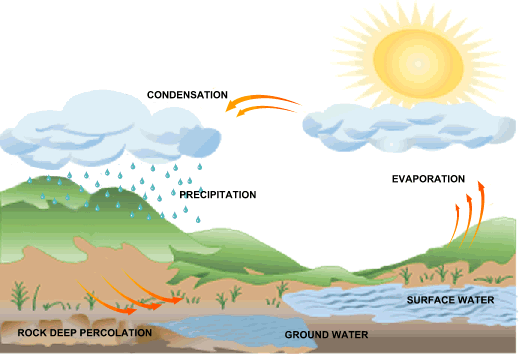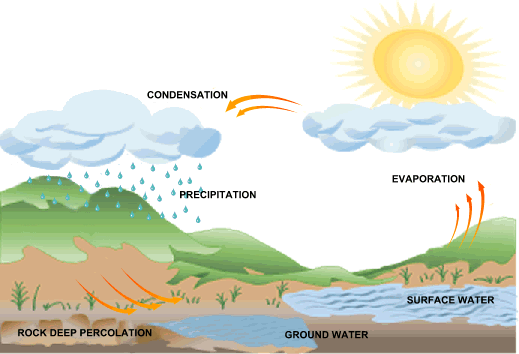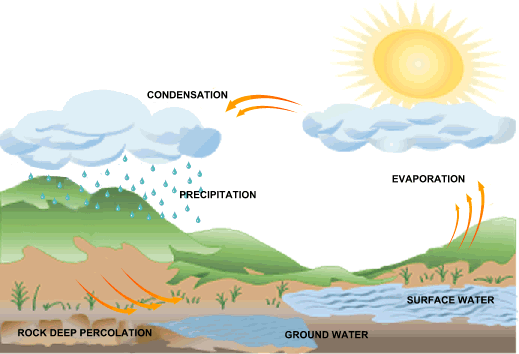
Changes to streamflow characteristics may benefit some aquatic organisms while harming others, thereby changing biotic community composition. For example, human activities may change how much water reaches a stream, divert flow through manmade channels (Figure 1) or alter stream shape and location.

Human activities can significantly alter flow and may lead to biological impairment. It may be appropriate to consider these different flow parameters as separate candidate causes.įlow alteration refers to modification of flow characteristics, relative to reference or natural conditions. Biological characteristics at a given site relate to flow volume, velocity and variance (including rates of change, frequency, duration and timing). Regional and temporal flow variability results from variance in rainfall patterns, vegetation, development, geology and other watershed characteristics. For both channel cross sections, however, discharge remains the same (assuming no inputs or diversions between the riffle and pool).įlow characteristics vary longitudinally along a stream's channel and laterally from channel to floodplain, as a function of landscape features. In the riffle, velocity is high, and in the pool immediately upstream, velocity is low. This distinction's significance becomes evident when considering multiple sites along a stream reach. Velocity can be thought of as a two-dimensional variable (length over time), whereas discharge is a four-dimensional variable (volume over time). Discharge is reported commonly as cubic meters per second (m 3/s), cubic feet per second (cfs), gallons per minute (gpm), or acre-feet per year (ac-ft/yr). We use the term “discharge” specifically in reference to volume as a function of time. We broadly define “flow” to include current velocity, volume as a function of time, large event frequency, and other parameters that characterize a flow regime. The terms “flow,” “discharge” and “streamflow” often are used interchangeably to represent water volume passing a fixed channel location per unit time. Movement of water through stream and river channels influences all processes and biota within. The Chesapeake and Ohio Canal National Historical Park, Washington D.C., an example of a channelized overland flow diversion. Finally, we replace this formula in the context of a conceptual stochastic rainfall-runoff model to find an expression for the return period of floods.Figure 1. We show that the binomial heuristic is a discrete approximation to the Poisson heuristic, and we provide a new expression to estimate the return period of hydrological extreme events through the Rice formula for level crossing counting of a continuous stochastic process. Here, we use the Poisson clumping heuristic to give an interpretation of the return period in the framework of continuous-time Markov processes, extending this concept to events separated by continuous inter-arrival times. On the other hand, there are available modern mathematical techniques to formulate questions about large deviations in random processes in terms of sparse random sets. However, this approach is not adequate for hydrological modeling because observations of hydrological variables do not necessarily represent independent Bernoulli trials. This traditional interpretation of the concept relies on a binomial heuristic since the return period is the expected value of a binomial random variable representing the time to the first success in a sequence of Bernoulli trials. If a random variable representing a hydrological process is measured every fixed time interval, and assuming that those observations are independent and identically distributed, then the return period of an extreme event is defined as the inverse of its probability of occurrence. In classical hydrology literature, an extreme event occurs when a random variable is greater or equal than a certain threshold.
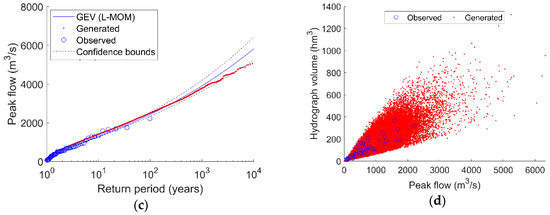
In this work, we propose a novel formulation of the return period in the context of time-continuous stochastic processes and introduce a new expression to estimate it under the assumptions of a conceptual stochastic rainfall-runoff model. The return period is a fundamental concept in hydrological engineering and risk analysis.


 0 kommentar(er)
0 kommentar(er)
